Mở đầu
Tiếp theo phân tích về Homography và Projection matrix ở phần trước
( https://hoanglong187.blogspot.com/2022/09/6-sift-part-4-homographies-camera-models.html )
Ta tiếp tục nghiên cứu về cách ứng dụng của Homography trong bài toán 2 bức ảnh có cùng vật thể.
Bài toán
Chúng ta nhắc lại sự chuyển dịch của bức ảnh (được coi là planar object) ở 2 bức ảnh thì được coi là 1 homography - 1 transform biến 1 projective plane thành 1 projective plane khác
Ở đây chúng ta xét 2 bức ảnh dựa trên: 2 thế giới khác nhau, 2 tư thế khác nhau so với camera, 2 người chụp khác nhau (cấu tạo image plane khác nhau) và 2 camera khác nhau
Ta thừa nhận rắng, mỗi một plane có thể được xác định bởi 1 điểm d nằm trên đó cùng với 2 vector a và b independent (vuông góc). Tức là mọi điểm trên plane có thể vết dưới dạng
Vậy đầu tiên ta cần tính 1 transformation T biến đổi 2 plane của 2 bức ảnhTa có thể viết lại rằng:(A1 và A2 là 3x3 matrix)
Với giả sử X1 và X2 nằm cùng vị trí ứng mỗi plane
Vậy ta cần tính X2 = T X1
hay:
Vậy ta có thể tính bất kì point nào từ 1 projective plane đến projective plane thứ 2 mà không cần biết vị trí 3D của point đó cũng như camera parameters
Rotate camera với góc R tương đương rotate 3D points với RT
Đây chính là phương trình homography!
Còn nếu ta tịnh tiến (translation) camera X2 = X1 - t
Mỗi giá trị của w1 sẽ cho ta điểm khác nhau trên bức ảnh thứ 2. Vì vậy dù có K và t, ta cũng không tính được hình chiếu của point từ ảnh đầu đến ảnh thứ 2Vì vậy: Việc nối các điểm của 2 bức ảnh phụ thuộc vào 3D scene (hoàn cảnh) đằng sau bức ảnh
Tuy nhiên, ngược lại nếu ta biết vị trí 2 điểm, ta có thể biết được vị trí 3D (gọi là Stereo, đưa chúng ta đến two-view geometry)
Sumary
Đi sâu hơn về 3D Scene Behind
Các phương thức tìm Depth từ Monocular Image:
- Shape from Shading - Shape from Texture - Shape from Focus/De-focus
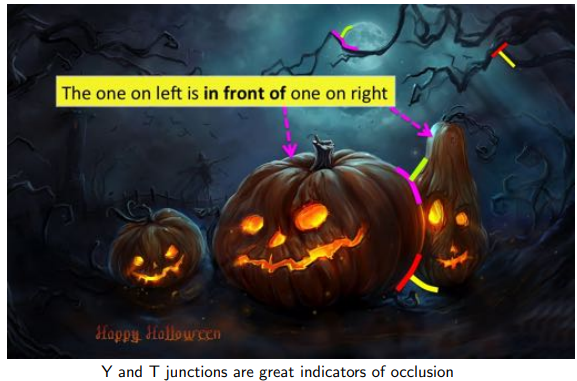
- Depth Ordering / Occlusion Reasoning - Depth from Google (Google app information)
- Depth via Recognition
- Depth via Machine Learning
- Depth by Tricking Brain :)
Tham khảo
- http://www.cs.toronto.edu/~fidler/slides/2021Winter/CSC420/lecture11.pdf





















Nhận xét
Đăng nhận xét