Mở đầu
Nghiên cứu về Epipolar Geometry - Stereo để hiểu thêm cac phép transform và homographic
Chúng ta có thể lấy được vị trí 3D với ảnh của point trên 2 image
Chúng ta chia thành 2 trường hợp dựa vào tính chất của 2 camera và image plane
Parallel Calibrated Cameras
Trong trường hợp này, ta biết intrinsic và extrinsic của 2 camera là như nhau. Ta gọi khoảng cách giữa 2 camera là baseline.
Với 2 camera có intrinsic và extrinsic, ta tính được vị trí tương đối của object 3D bằng đơn vị pixel. Vì vậy cần thêm yêu tố baseline để tính được so với vị trí teo world
Các điểm Ol Or và P (cả Pl và Pr) đều nằm trên 1 plane. Trong khi 2 image plane trùng nhau và đều có khoảng cách f với mỗi camera (tức OlOr song song PlPr). Do đó Ta xây dựng hình chiếu của Olpl trên right image plane dựa vào Or thì vẫn sẽ là 1 đường trùng với đường plpr
Từ đó ta dễ dàng dùng định lí Talet trong hình học phẳng hay tam giác đồng dạng để tính được Z Sau đó sử dụng Z để tính được X và Y, từ đó có tọa độ 3DTa ứng dụng với cặp camera song song:Tại mỗi point trên scanline, ta tính matching cost (thường là SSD hoặc normalized correlation)
Đã có 1 model đã làm tốt hơn dựa vào CNN và cách phân chia positive (match đúng) và negative (match sai)Làm với mọi points ở left image, ta được Disparity map
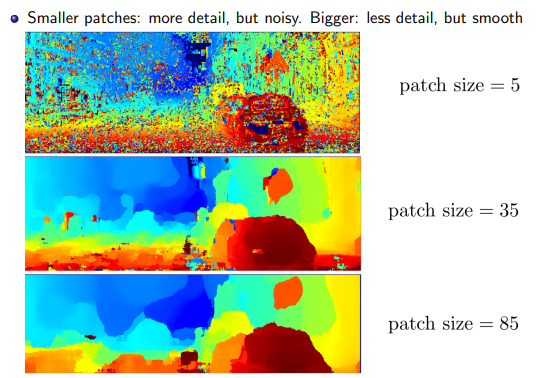
Ta thấy rằng dựa vào bảng đồ này cũng thấy được nơi nào xa, nơi nào gần so với camera
Tuy nhiên cũng cần chỉnh tham số patch phù hợp
Epipolar Geometry - General Cameras
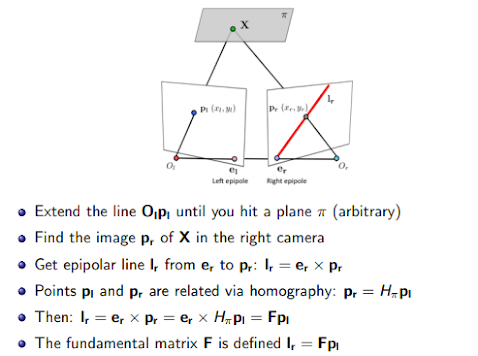
Trường hợp này 2 image plane sẽ không trùng nhau, nên ta có line hình chiếu (epipolar line) cũng không song song hay trùng nhau
Ta gọi plane bởi 3 điểm Ol, Or và P là epipolar plane, chứa cả 2 epipolar line
Quan sát rằng với mỗi 3D points khác nhau sẽ tạo các epipolar line khác nhau, nhưng vẫn đều đi qua các epipole point (left epipole và right epipole)
Tương tự cũng hoạt động với trường hợp đi thẳng
Ta thấy rằng dựa vào bảng đồ này cũng thấy được nơi nào xa, nơi nào gần so với camera
Tuy nhiên cũng cần chỉnh tham số patch phù hợp
Epipolar Geometry - General Cameras
Trường hợp này 2 image plane sẽ không trùng nhau, nên ta có line hình chiếu (epipolar line) cũng không song song hay trùng nhau
Ta gọi plane bởi 3 điểm Ol, Or và P là epipolar plane, chứa cả 2 epipolar line
Quan sát rằng với mỗi 3D points khác nhau sẽ tạo các epipolar line khác nhau, nhưng vẫn đều đi qua các epipole point (left epipole và right epipole)
Tương tự cũng hoạt động với trường hợp đi thẳng
Ta sẽ chứng minh rằng có thể tìm match point của mỗi điểm tại left image thông qua 1 matrix 3x3 F, gọi là Fundamental matrix. Dựa vào F, ta có thể biến các epipolar lines thành horizontal
Chứng minh:Tiếp theo ta có
F có 9 phần tử, trừ scalling thì còn 8, thực chất chỉ có 7. Tức ta có thể tối ưu F chỉ với 7 matchs, nhưng càng nhiều càng tốt (lỗi sai số, regression)
Khi đã có F, ta có thể tính được homographies để chuyển mỗi image plane thành dạng parallel. Đến đây ta xử lí như trường hợp trước
Ngoài ra, khi đã có F, ta cũng có thể tính Pl và Pr (với việc thêm 1 vài ambiguity).Tức là ta không cần biết trước pose (tư thế) cảu planar object so với camera, ta có thể tính nóKhi đã có F, ta có thể tính được homographies để chuyển mỗi image plane thành dạng parallel. Đến đây ta xử lí như trường hợp trước
Qua biểu thức, để tính Pr, ta chỉ cần thêm er. Ta có er nằm trên epipolar line lr, vậy Mà
vậy
Summary
Tham khảo
- https://www.youtube.com/watch?v=PFQ3A7TEMIo&ab_channel=PratikJain
- http://www.cs.toronto.edu/~fidler/slides/2021Winter/CSC420/lecture12.pdf
- https://www.youtube.com/watch?v=izpYAwJ0Hlw&ab_channel=FirstPrinciplesofComputerVision
- http://www.cs.toronto.edu/~fidler/slides/2021Winter/CSC420/lecture13.pdf


















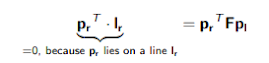









Nhận xét
Đăng nhận xét